Illustration of a knight tour on an 8x8 chessboard.
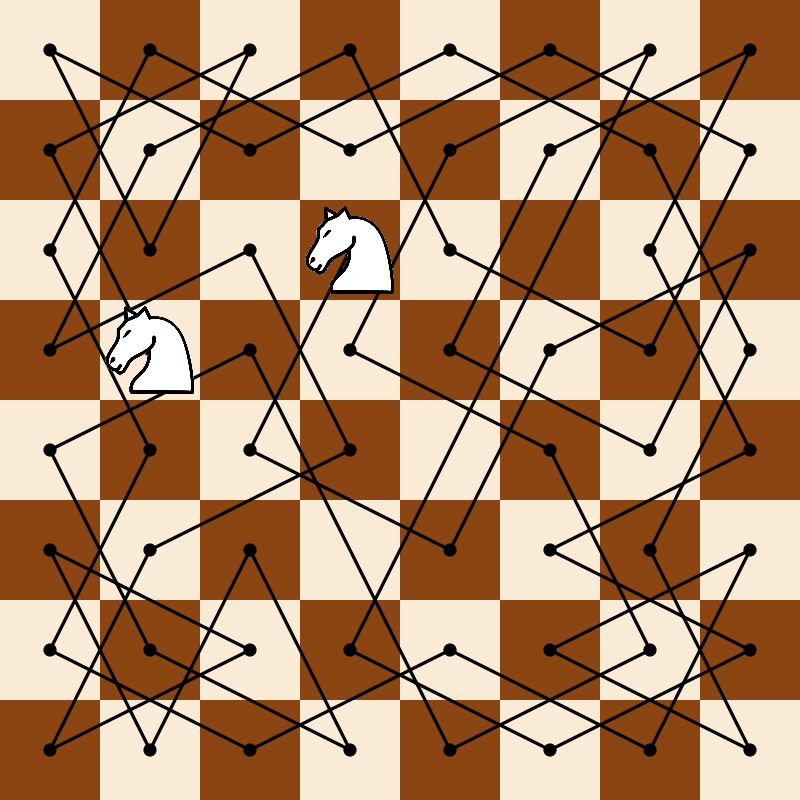
import Diagrams.Backend.SVG.CmdLineA relatively well-known puzzle is to find a sequence of moves by which a knight can visit every square of a chessboard exactly once, without repeating any squares. This example computes such a tour and visualizes the solution.
{-# LANGUAGE NoMonomorphismRestriction #-}
import Data.List (minimumBy, tails, (\\))
import Data.Ord (comparing)
import Diagrams.PreludeFirst, we compute a tour by a brute force depth-first search (it does not take very long). This code is adapted from the code found here.
type Square = (Int, Int)
board :: [Square]
board = [ (x,y) | x <- [0..7], y <- [0..7] ]
knightMoves :: Square -> [Square]
knightMoves (x,y) = filter (`elem` board) jumps
where jumps = [ (x+i,y+j) | i <- jv, j <- jv, abs i /= abs j ]
jv = [1,-1,2,-2]
knightTour :: Square -> [Square]
knightTour sq = knightTour' [sq]
where
knightTour' moves@(lastMove:_)
| null candMoves = reverse moves
| otherwise = knightTour' $ newSquare : moves
where newSquare = minimumBy (comparing (length . findMoves)) candMoves
candMoves = findMoves lastMove
findMoves s = knightMoves s \\ movesNow we can go about visualizing a tour. First, let’s draw a chessboard:
boardSq :: Colour Double -> Diagram B
boardSq c = square 1 # lw none # fc c
chessBoard :: Int -> Diagram B
chessBoard n
= vcat . map hcat . map (map boardSq)
. take n . map (take n) . tails
$ cycle [antiquewhite, saddlebrown]Now, we need a way to convert Square coordinates (a pair of numbers
in the range 0-7) into actual coordinates on the chessboard. Since
the chessboard ends up with its local origin in the center of the
top-left square, all we need to do is negate the \(y\)-coordinate:
squareToPoint :: Square -> P2 Double
squareToPoint (x,y) = fromIntegral x ^& negate (fromIntegral y)To draw a knight on a given square, we simply translate the given image appropriately:
knight :: Square -> Diagram B -> Diagram B
knight sq knightImg = knightImg # moveTo (squareToPoint sq)Given a tour, we turn it into a path using fromVertices,
and decorate the vertices with dots.
drawTour :: [Square] -> Diagram B
drawTour tour = tourPoints <> strokeP tourPath
where
tourPath = fromVertices . map squareToPoint $ tour
tourPoints = atPoints (concat . pathVertices $ tourPath) (repeat dot)
dot = circle 0.05 # fc blackFinally, we load a knight image, size it to fit a square, and then put all the previous pieces together:
example = do
res <- loadImageEmb "doc/static/white-knight.png"
let knightImg = case res of
Left _ -> mempty
Right img -> image img # sized (mkWidth 1)
return $ mconcat
[ knight tourStart knightImg
, knight tourEnd knightImg
, drawTour tour
, chessBoard 8
]
where
tourStart = (1,3)
tour = knightTour tourStart
tourEnd = last tourmain = mainWith (example :: Diagram B)