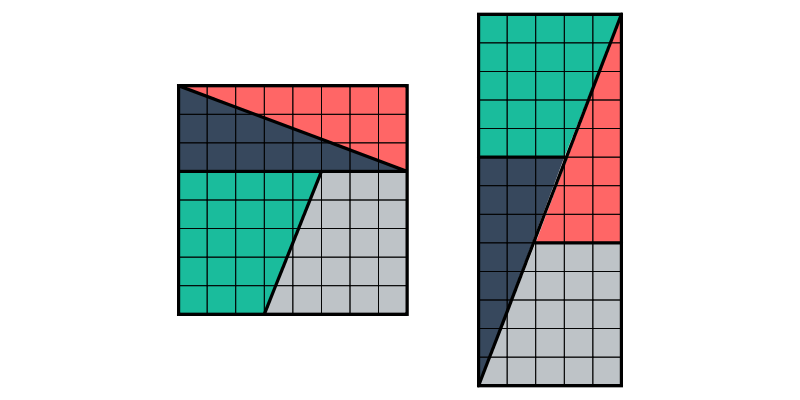
A favorite puzzle/paradox of Lewis Carroll based on Fibonacci numbers. The two figures are “obviously” composed of the same pieces, yet they have different areas!
import Diagrams.Backend.SVG.CmdLine{-# LANGUAGE NoMonomorphismRestriction #-}
import Diagrams.Prelude hiding (tri)
import Data.Colour.SRGB (sRGB24read)The standard infinite list of Fibonacci numbers.
fibs :: [Int]
fibs = 0 : 1 : zipWith (+) fibs (tail fibs)Create a grid by gluing together a bunch of squares.
grid :: Int -> Int -> Diagram B
grid x y = frame <> lattice
where s = unitSquare # lw thin
frame = rect (fromIntegral x) (fromIntegral y)
# lw thick
lattice = centerXY . vcat . map hcat . replicate y . replicate x $ sThe trapezoid and triangle shapes, with sides lengths based on two Fibonacci numbers.
trap, tri :: Double -> Double -> Diagram B
trap s1 s2 = lw none . strokeLoop . closeLine
. fromOffsets . map r2 $ [(0,-s2), (s2,0), (0,s1)]
tri s1 s2 = lw none . strokeLoop . closeLine
. fromOffsets . map r2 $ [(s1,0), (0,s1+s2)]Draw the paradox diagram based on the nth Fibonacci number.
paradox :: Int -> Bool -> Diagram B
paradox n drawDiags = (sq # rotateBy (1/4)
||| strutX (s2 / 2)
||| rect # rotateBy (1/4)) # centerXY
where f1 = fibs !! n
f2 = fibs !! (n+1)
s1 = fromIntegral f1
s2 = fromIntegral f2
trap1 = trap s1 s2 # fc (sRGB24read "#BEC3C7")
trap2 = trap s1 s2 # fc (sRGB24read "#1ABC9C")
# rotateBy (1/2)
tri1 = tri s1 s2 # fc (sRGB24read "#FF6666")
tri2 = tri s1 s2 # fc (sRGB24read "#37485D")The four shapes assembled into a square.
sq = (if drawDiags then sqDiags else mempty)
<> grid (f1+f2) (f1+f2)
<> sqShapes
sqDiags = (fromVertices [p2 (0,s2), p2 (s2,s1)] <>
fromVertices [p2 (s2,0), p2 (s2,s1+s2)] <>
fromVertices [p2 (s2,0), p2 (s1+s2,s1+s2)])
# strokeP
# lw thick
# centerXY
sqShapes = (traps # centerY ||| tris # centerY)
# centerXY
traps = trap2 # alignL
# translateY (s1 - s2)
<> trap1
tris = tri1 # alignBL
<> tri2 # rotateBy (1/2)
# alignBLThe four shapes assembled into a rectangle.
rect = (if drawDiags then rDiags else mempty)
<> grid (2*f2 + f1) f2
<> rShapes
rShapes = (bot # alignTL <> top # alignTL) # centerXY
bot = trap1 # alignB ||| rotateBy (-1/4) tri1 # alignB
top = rotateBy (1/4) tri2 # alignT ||| trap2 # alignT
rDiags = (fromVertices [p2 (0,s2), p2 (2*s2+s1, 0)] <>
fromVertices [p2 (s2,0), p2 (s2,s1)] <>
fromVertices [p2 (s1+s2,s2-s1), p2 (s1+s2,s2)]
)
# strokeP
# lw thick
# lineCap LineCapRound
# centerXYDraw the order-4 diagram with thick lines in the middle. Passing the
argument False causes the thick lines to be omitted, revealing the
skinny gap in the rectangular assembly. Lower-order diagrams make the
gap more obvious; higher-order diagrams make it increasingly less
obvious (but make the grid smaller).
example = paradox 4 True # frame 0.5main = mainWith (example :: Diagram B)