Diagrams - Imperial Seal of Japan

Code to generate the Imperial Seal of Japan, a stylized chrysanthemum with 16 petals.

Author: Timo Abele

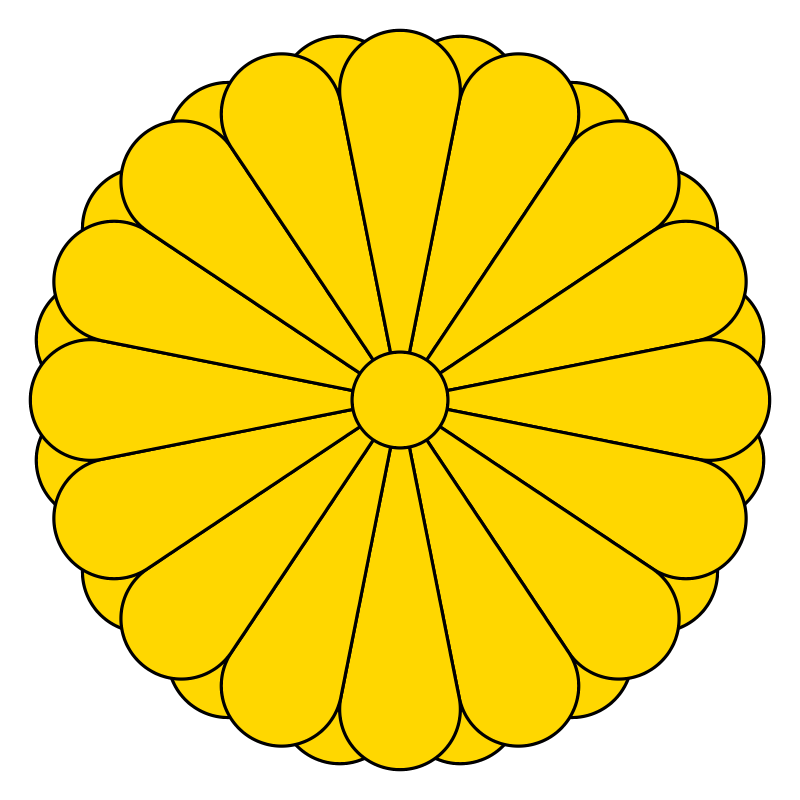
import Diagrams.Backend.SVG.CmdLine

import qualified Diagrams.TwoD.Path.Boolean as B

We start with an upright petal defined by an angle. We construct the petal from a wedge and a circle which we position in such a way that the circle touches the wedge right and left of the circle segment.

petal :: Angle Double -> Diagram B
petal angle = strokePath $ B.union Winding (uprightWedge <> touchingCircle)
 where

First we draw an upright wedge by constructing a counterclockwise wedge starting at 12 o’clock, then rotating it clockwise so it is centered.

   uprightWedge = wedge 1 yDir angle # rotate (negated halfAngle)

Next, we draw the circle touching the wedge.

   touchingCircle = circle circleRadius # translateY yShift

The center (origin) of the wedge, the center of the circle and the point where they touch form a right-angled triangle with the hypotenuse being the line from center_circle to center_wegde, and relative to half the wedge’s angle at the origin of the wedge, the adjacent leg is radius_wedge and the opposite opposite leg is radius_circle. Thus, cos halfAngle = radius_wedge(=1) / hypotenuse

   yShift  = 1 / cosA halfAngle

and tan halfAngle = radius_circle / radius_wedge.

   circleRadius = 1 * tanA halfAngle
   halfAngle = (/2) <$> angle

For the corolla we want n petals arranged in a circle so each has an angle of 1/n times a full circle.

nPetals n = mconcat $ take n $ iterate (rotate angle) (petal angle)
 where
   angle = (1 / fromIntegral n) @@ turn

The seal consists of two corollas on top of each other with a small circle on top of them.

imperialSeal = circle 0.158
               <>                                  corolla
               <> rotateBy (1/ fromIntegral (2*n)) corolla
                  -- background corolla rotated by half a petal
         where
           corolla = nPetals n
           n = 16

imperialSealGoldWhite = imperialSeal # fc gold
                                     # bgFrame 0.1 white

imperialSealGoldRed = imperialSeal # fc (sRGB24read "#c0a73f")
                                   # lc (sRGB24read "#be0025")
                                   # bgFrame 0.1 (sRGB24read "#be0025")
                                   # lwG 0.04

example = imperialSealGoldWhite

main = mainWith (example :: Diagram B)