Diagrams - Tangent and normal

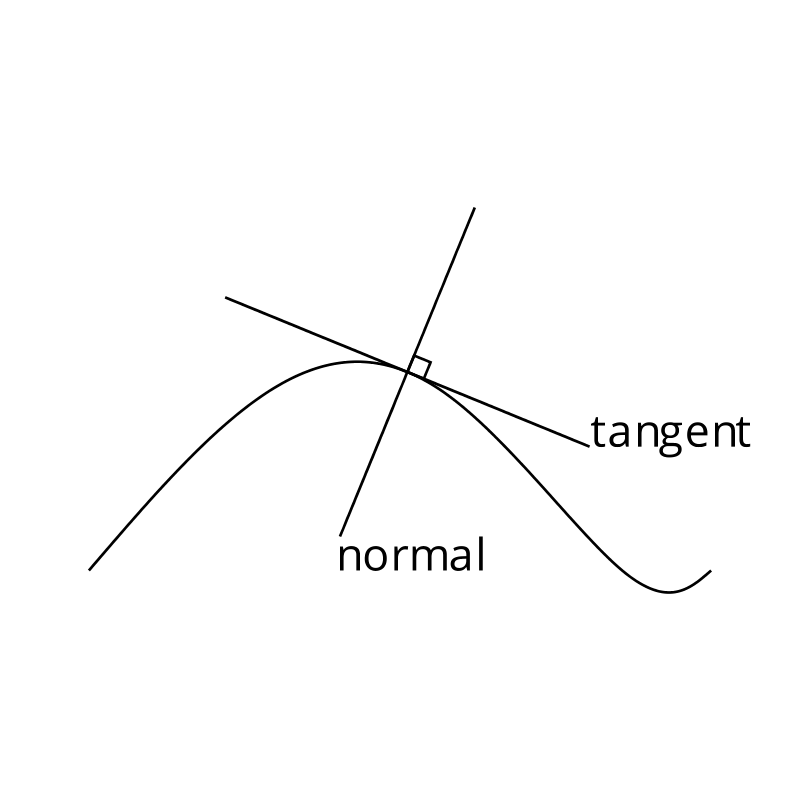
Illustrating the tangent and normal vectors to a point on a curve.

Author: Pontus Granström

import Diagrams.Backend.SVG.CmdLine

import Diagrams.Prelude

Some arbitrary points, with a cubic curve passing through them.

pts = map p2 [(0,0), (1,1), (2,1), (3,0), (3.5,0)]

spline :: Located (Trail V2 Double)
spline = cubicSpline False pts

Computing tangent and normal vectors at a particular point on the curve.

param = 0.45 -- parameter on the curve where the tangent and normal are drawn
pt = atParam spline param
tangentVector = tangentAtParam spline param
normalVector = normalAtParam spline param

We can draw the tangent and normal vectors with lines of twice their length, with a square in between them to denote the right angle.

symmetricLine v = fromOffsets [2 *^ v] # center
tangentLine = symmetricLine tangentVector
normalLine = symmetricLine normalVector

rightAngleSquare = square 0.1 # alignBL # rotate (signedAngleBetween tangentVector unitX)

Putting it all together, with some labels.

example :: Diagram B
example = frame 0.5 $
  strokeLocTrail spline
  <> mconcat
     [ tangentLine
     , baselineText "tangent" # translate tangentVector
     , normalLine
     , topLeftText "normal" # translate normalVector
     , rightAngleSquare
     ] # moveTo pt # fontSize large

main = mainWith (example :: Diagram B)